quarta-feira, julho 18, 2007
Algorítmos de Ordenação - Parte IV
Ordenação por Incrementos Decrescentes - Shell Sort
Este algorítmo foi inventado por Donald L. Shell, e se baseia na idéia de que podemos ordenar mais rápido se começarmos movendo as chaves distâncias maiores, para que eles cheguem mais rapidamente nas posições finais.
Para usar o Shell Sort, você precisa ter ou gerar uma lista de incrementos decrescentes, onde o último é um. Iniciamos a ordenação ordenando os elementos espaçados pelo primeiro (e maior) incremento. Em seguida, ordenamos os elementos espaçados do segundo incremente e assim por diante. No último passo ordenamos os elementos espaçados de 1, ou seja, todos os elementos. Nos primeiros passos estamos ordenando conjuntos com poucas chaves mas bem diferentes, no final estamos ordenando conjuntos com muitas chaves mas quase totalmente ordenadas. Por este motivo podemos usar a inserção direta para a ordenação de cada conjunto.
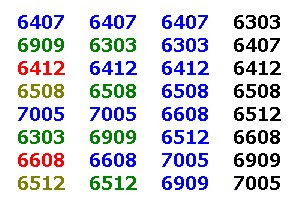
Confuso? Vamos a um exemplo, ordenando 8 números usando os incrementos 4, 2 e 1. Vamos ter portanto 3 passos: no primeiro ordenamos 4 conjuntos de 2 chaves, no segundo 2 conjuntos de 4 chaves e no último um único conjunto com as 8 chaves. A figura abaixo mostra os dados originais e o resultado de cada passo.
A análise do desempenho deste algorítmo é muito complexa. A escolha dos incrementos é um ponto chave, mas não é simples determinar qual seria uma boa escolha. Knuth sugere como razoável a série 1, 4, 14, 40, 121, etc, na qual cada número é igual a três vezes o anterior mais um. A série deve parar dois números antes de ultrapassar o número de itens a ordenar. Por exemplo, para ordenar 100 itens usaríamos 1, 4 e 13. Usando estes tempos, o tempo médio é proporcionala N1.25 e pior caso proporcional a N1.5. Memória adicional pode ser necessária para guardar os incrementos (se os calcularmos antecipadamente), a série sugerida possui log3(N) incrementos. O Shell Sort não é estável.
Na próxima parte desta série vamos ver o algoritmo mais conhecido de ordenação (pelo menos no nome) - o Quicksort.
06/08/07: Acertados os subscripts e superscripts.
terça-feira, julho 17, 2007
Divagações sobre Efetividade, Eficiência e Eficácia
O que é Efetividade?
Há muito tempo atrás, se ouvia que eficiência era fazer bem alguma coisa e eficácia era fazer bem a coisa certa. E a onde entra a efetividade? Uma rápida consulta à wikipedia me faz crer que a efetividade é atualmente usada como equivalente ao que eu conhecia como eficácia. A eficácia foi rebaixada a fazer a coisa certa enquanto que a eficiência continua relacionada a fazer bem (com bom aproveitamento dos recursos).
Por trás de toda estas palavras e definições está uma grande questão: determinar o que é A Coisa Certa. A necessidade destas múltiplas palavras se deve principalmente a termos situações frequentes em que alguém (ou algo) fez tudo certo (por uma definição) e o resultado foi errado. Ou vice-versa (compare a seleção brasileira na copa de 82 com o time do Dunga na Copa América).
Métricas é uma Solução?
Métricas são sempre apresentadas como uma solução, muitas vezes até como algo essencial. Embora eu acredite na necessidade e na utilidade de métricas, cada vez questiono mais a crença da métrica como solução.
Estou lendo (bem devegar, há muito tempo) um livro chamado "Measuring and Managing Performance in Organizations", de Robert D. Austin (indicação do Joel On Software). Resumindo a teoria apresentada, usamos métricas para incentivar pessoas a fazerem A Coisa Certa. Entretanto, as pessoas vão procurar otimizar as métricas (até o ponto em que isto não compense frente aos incentivos) e acabar por se distanciar dA Coisa Certa (o que o autor chama de Dysfunction). Se você remunera o vendedor pelo volume do faturamento, ele concede descontos demais; se você o remunera por margem, ele atende mal clientes importantes por outros motivos (volume, boa referência para o mercado, etc); se você cria a "formula perfeita", provavelmente ela é tão complicada que o vendedor não vai se dar ao trabalho de entender e vai fazer o que quiser enquanto estiver obtendo uma remuneração satisfatória.
O Curto, o Médio e o Longo Prazo
No início do curso de Engenharia, um professor disse que a essência da Engenharia era achar o compromisso correto. Isto vale para a maioria das coisas. É frequente termos que optar entre uma solução rápida e barata que resolve o problema agora, mas vai trazer problemas mais para frente, e uma solução mais complexa e cara que achamos que vai ser mais tranquila no futuro. Qual destas soluções é mais efetiva?
Uma situação do meu dia a dia é quando me pego fazendo algo repetitivo. Será que é melhor fazer um programa (ou script) para automatizar isto? Em alguns casos continuo até hoje fazendo coisas manualmente. Em outros eu investi algum tempo e fiz uma solução automática que me traz um sorriso nos lábios toda vez que uso. Porém existem casos em que perdi muito tempo fazendo um destes programas auxiliares que está encostado sem uso em algum canto do meu HD.
As Interrupções
É inegável que o meu rendimento (e a qualidade do trabalho) aumenta quando me concentro em uma única coisa. Por outro lado, isto aumenta o tempo de resposta para as outras, o que irrita quem está esperando por elas. Aliás, o simples fato de achar que os outros vão ficar irritados acaba me irritando.
O mundo atual quer o instantâneo. Você pede para a pessoa enviar solicitações por e-mail e a pessoa liga dali a 5 minutos para perguntar se você recebeu o e-mail. Se você não atende o telefone, ligam no celular ou ligam para quem está no lado. No final, será que ser interrompido constantemente é mais efetivo que tentar bloquear o mundo por algumas horas?
Um dos artigos interessantes concorrendo na promoção do Efetividade.net é o Frango Tosco. Um ponto que me preocupou: a preparação demora cerca de 75 minutos, dividida em 6 passos sinalizados pelo apito do microondas. Para mim isto não funcionaria, estas seis interrupções me deixariam louco (sem contar que eu provavelmente ia xeretar entre elas, só para me certificar que está tudo correto).
Concluindo
Como avisei no início, este artigo não traz soluções. Não tenho a resposta para as perguntas que fiz e nunca estou plenamente satisfeito com as opções que fiz. A única coisa positiva que posso dizer é que me sinto mais satisfeito questionando as opções do que seguindo cegamente uma lista de regras.
segunda-feira, julho 16, 2007
Algorítmos de Ordenação - Parte III
Straight Insertion Sort (Ordenação por Inserção Direta)
Este é um dos mais simples algorítmos de ordenação e funciona como um jogador de cartas organizando a sua mão. Durante a execução deste algorítmo, as primeiras chaves estão ordenadas (no início esta parte esta vazia, no final todas as chaves foram ordenadas). Pegamos a primeira chave ainda não ordenada e achamos o seu lugar nas já ordenadas e a inserimos aí. Repetimos isto até que todas as chaves estejam ordenadas (ver a Figura 1) Este algorítmo pode levar a muitas movimentações de chaves, principalmente se elas estiverem em ordem inversa no início. Ele é bastante simplas de codificar, não requer memória adicional e é estável. É evidente que os tempos médio e máximo são proporcionais a N2.
Bubble Sort (Ordenação por Bolhas)
 Figura 2 - Ordenando com o Bubble Sort (passo final)
Figura 2 - Ordenando com o Bubble Sort (passo final)Na próxima parte vamos ver um algorítmo menos comum, o Shell Sort.
domingo, julho 15, 2007
Algorítmos de Ordenação - Parte II
Alguns critérios normalmente usados para comparar algorítmos de ordenação são:
- Velocidade de execução
- Necessidade de Memória Adicional
- Estabilidade
Velocidade de Execução
Este é normalmente o critério mais importante. Não se pode, entretanto, esquecer que a velocidade vai depender de vários fatores.
É intuitivo que quanto mais itens temos para ordenar, mais tempo vai demorar. A forma como o tempo aumenta com o aumento dos itens varia conforme o algorítmo.
Considere o sequinte algorítmo simples: examinamos os N itens, um a um, e separamos o primeiro; repetimos o processo para os N-1 intens restantes e assim por diante. A ordenação levará N+(N-1)+(N-2)+...+1 passos. Esta soma resulta em N2/2 passos, daí dizermos que este algorítmo leva um tempo proporcional a N2 para ordenar N itens. Veremos nos próximos artigos que um bom algorítmo reduz isto para N*log(N) passos. Na maioria dos casos, quanto melhor o algorítmo, mais complexos serão os passos e portanto eles serão mais demorados. Mesmo assim, para um N grande log(N) é muito menor que N.
Por exemplo, vamos supor que temos um programa que demora N2 microsegundos para ordenar N itens e outro que leva 100*N*log(N) microsegundos (em outras palavras, cada passo do segundo programa demora 100 vezes mais que cada passo do primeiro).
Para ordenar 10 itens, o primeiro algorítmo demora 100 microsegundos e o segundo 1000 microsegundos. Ordenando 100 itens, os tempos sobem para 10000 e 20000 microsegundos. Para 1000 itens, o primeiro levará 1000000 de microsegundos (mais de 16 minutos), enquanto que o segundo levará apenas 300000 (5 minutos).
Não é o caso do algorítmos simples apresentado acima, mas o tempo para os algorítmos mais sofisticados vai depender dos dados serem ordenados. Isto nos obriga a falar em tempo médio e em tempo do pior caso. Por exemplo, veremos que o Quicksort possui um tempo médio proporcional a N*log(N) e um tempo do pior caso proporcional a N2. Isto significa, que o Quicksort é normalmente muito rápido, porém às vezes é muito lento!
A velocidade depende também das características do computador. A ordenação envolve principalmente comparar e mover chaves. Computadores diferentes podem levar tempos relativos diferentes para estas duas operações. Por exemplo, suponha que as chaves sejam valores em ponto flutuante. Pode existir uma grande diferença nas velocidades de comparação entre um computador com unidade de ponto flutuante e um computador que necessite fazer uma chamada de biblioteca. Neste segundo computador pode fazer sentido minimizar as comparações, mesmo que isto signifique mais movimentações. O resumo da história é que um algorítmo que funcione bem num computador pode não se dar tão bem em outro.
Necessidade de Memória Adicional
Alguns algorítmos são capazes de ordenar os dados nas posições em que eles estão armazenados, usando memória adicional apenas para trocar de posição duas chaves. Outros necessitam de memória adicional proporcional ao tamanho dos dados sendo ordenados. Os algorítmos descritos nesta série necesitam de nenhuma ou muito pouca memória adicional.
Estabilidade
Dizemos que um algorítmo é estável se ele manter chaves iguais na mesma ordem em que elas estão na entrada. Dizendo de outra maneira, se nós aplicarmos o algorítmo a dados já ordenados, a saída será idêntica à entrada. É sempre possível converter um algorítmo instável em um estável usando a posição original da chave como o último critério de ordenação. Por exemplo, se estamos usando ponteiros para ordenar as chaves, comparamos os ponteiros se as chaves são iguais.
No próximo artigo da série vamos ver os primeiros algorítmos de ordenação.
quinta-feira, julho 12, 2007
Algorítmos de Ordenação - Parte I
Introdução
Comecei a escrever a primeira versão deste texto em inglês, em 2000, mas nunca cheguei a concluir. Para quem tiver curiosidade, aqui está a versão do texto que encostei em 2002.
Ordenar coisas é uma tarefa comum na programação. É também um daqueles tipos de tarefas onde o algorítmo utilizado faz uma grande diferença. Os exemplos que vão acompanhar esta série, além de conterem implementações dos algorítmos descritos, vai ajudar a ver como eles funcionam e comparar o desempenho deles.
Ordenação também é o tipo de tarefa que clama por uma boa análise matemática. Você não vai encontrar isto aqui! A "bíblia" da ordenação, na minha opinião, é o livro "The Art of Computer Programming, Vol 3 - Sorting and Searching" de Donald E. Knuth. Foi com este livro que aprendi o que apresento aqui. Alguns podem achar o estilo do Dr Knuth ultrapassado (implicando com os exemplos em linguagem assembler de um computador hipotético), mas dificilmente se acha um texto tão completo como o dele.
Por último, muitas linguagens possuem em sua biblioteca padrão funções genéricas de ordenação e muitos preferem simplesmente as usar sem conhecer como funcionam. Como veremos, existem vários pontos interessantes sobre a ordenação e nem sempre a escolha de um algorítmo é simples. Mesmo que você nunca precise escrever a sua própria função de ordenação, muito pode ser aprendido estudando estes algorítmos.
O Que é Ordenar?
Basicamente, estamos falando em colocar coisas em uma certa ordem. Nós temos itens (ou registros) a serem ordenados. Cada item está associado a uma uma chave. Nosso objetivo é re-arranjar os itens de forma que eles fiquem em ordem crescente (ou decrescente) de chave.
Nesta série vamos nos concentrar em ordenar um vetor de chaves numéricas (inteiras) que estão na memória. As idéias apresentadas podem ser facilmente expandidas:
- Podemos usar os mesmos algorítimos com qualquer tipo de chaves. Tudo que precisamos é uma forma de comparar as chaves e uma maneira de movê-las. Por exemplo, podemos ter chaves alfanuméricas e ordená-las sem considerando maiúsculas e minúsculas como equivalentes (de forma que 'aBc' seja igual a 'AbC' ou 'ABC')
- Podemos ter múltiplas chaves. Se as primeiras chaves são iguais, nós comparamos as segundas e assim por diante até acharmos uma diferença ou testarmos todas as chaves. Se as chaves forem alfanuméricas, podemos fazer isto simplesmente as concatenando. Se misturarmos chaves de tipo diferente, nossa comparação pode usar o operador && do C (ou construção equivalente de outra linguagem) para testar as chaves na ordem correta.
- Ao mesmo tempo em que ordenamos as chaves, ordenamos os registros. Se os registros forem pequenos, simplesmente os movemos junto com as chaves. Se os registros forem grandes, nós guardamos ponteiros para os registros junto com as chaves. Durante a ordenação, movemos junto as chaves e os ponteiros. Ao final seguimos os ponteiros para obter os registros na ordem certa (veja Figura 1).
- Se as chaves não cabem na memória, fazemos a ordenação por partes, gravando as partes em arquivos temporários. Ao final fazemos um merge das partes (ver Figura 2).
Republicando artigos meus da Sharepedia
Animal
Um exemplo simples (bobo ?) de uso de árvore binária: um jogo de adivinhação de animais. A árvore consiste em vária perguntas do tipo Sim / Não, onde as folhas são animais. O programa vai percorrendo a árvore (fazendo as perguntas e obtendo as respostas). Ao chegar em uma folha, pergunta se este é o animal que o jogador pensou. Se não for, pergunta qual o animal e pede uma pergunta para distinguí-lo da resposta errada. A árvoré é então atualizada com a nova pergunta e o novo animal.
Arquivo
Avisa se esqueceu disco na unidade
CDAlert é um pequeno utilitário que testa se existe disco removível quando é feito shutdown. Ilustra como descobrir as unidades existentes e seus tipos, através da API Win32.
Arquivo
Aviso (Recado tipo Post-It)
Este é um programinha simples para colocar uma mensagem na tela. A mensagem pode ser colocada na linha de comando, chamando o programa sem parâmetro é apresentado um dialogo para digitacao da mensagem. A janela com a mensagem fica por cima das demais janelas e pode ser arrastada. Para fechá-la, basta dar um double click. Ilustra algumas técnicas menos comuns de programação Windows direto com a API.
Arquivo
Desenhando em Diálogo
O objetivo deste artigo é apresentar uma forma de desenhar gráficos em uma caixa de diálogo, utilizando diretamente a API do Windows. O artigo inclui um programa exemplo que mostra um relógio de ponteiros em um diálogo.
Arquivo
Como fazer um Editor Simples
Este exemplo ilustra três formas de criar um editor simples: usando um Edit Box, usando um Rich Edit controle e "na raça". O código está em C e usa apenas o Win32 SDK .
Arquivo
Launch - demo do uso de CreateProcess
Este programa mostra como usar a função CreateProcess da API do Windows para disparar uma aplicação.
Arquivo
Lista Ligada - O Guia dos Mestres
Este artigo explica a teoria e a prática das Listas Ligadas, com atenção particular à implementação em C e C++.
Arquivo
Exemplo de Uso de ListView
Exemplo de uso de ListView com imagens, usando C + API. Nova versão implementa ordenação pelo cabeçalho das colunas. Destaque para os infames dados usados no exemplo!
Arquivo
Screen Savers - "O Gua dos Mestres"
Uma descrição bem detalhada de como funciona e como fazer screen savers. Inclui dois exemplos, um usando a biblioteca Scrnsave.lib e o outro chamando direto as API do Windows.
Arquivo
Simulação de um Computador
Um exemplo (simples) de como simular um computador. O simulador apresenta na tela os registradores e a memória de um computador hipotético. Programas podem ser entrados em linguagem de máquina ou em assembler. Interessante para quem quer aprender um pouco sobre linguagem de máquina, sobre a simulação de computadores ou mesmo sobre programação Windows.
Arquivo
Threads & Sockets: exemplo de uso
Este código mostra como usar threads e sockets para fazer uma comunicação cliente/servidor.
Arquivo